Quantitative Aptitude Part – 3 includes TIME – SAVING METHODS in calculation. You must follow the Short-Cut, Time-Saving methods to quickly solve the questions in the Quantitative Aptitude Section. The Time-Saving Methods will enable you to attempt maximum number of questions in the limited time period during the actual examination..

TIME – SAVING METHODS

You must follow the below given Time – Saving Methods while solving the actual examination papers . You can master the calculation methods with a little of practice .

ADDITION

No doubt, addition of two or more numbers is a very simple process and almost all of us can do it. Yet, we can save a lot of time by the following simple ways :

A – 1 : We should not do addition by writing numbers longitudinally because in the examination paper questions requiring addition ( or subtractions, multiplication, division ) are given in a horizontal manner.

For example , for solving 20 +23 + 49 most of us shall first write it longitudinally as given below and then solve it :

This practice is indeed very time consuming and one must avoid it.

The proper way for solving this question would be like this : 20 + 23 + 49 = ?

Say, 0 +3 +9 = 12. Write 2 and carry 1 .
Then say, 1 (carried from 12 ) + 2 + 2 + 4 = 9 write this 9 on the left side of 2.
So, the answer is 92.

A – 2 : While doing addition of numbers containing more than two digits, one may follow the double column method.

For Example : 1424 + 3982 + 123

Solution : First underline the last two digits of every figure and then the question will look like this :

Note : Here, in order to clear the doubts, if any, regarding the digits to be carried , it may be said that if one is following the single column method of addition ( i.e. adding single digits at a time) then one would have to ‘Write’ only one digit ( which is at the unit place or at extreme right ) and the remaining digit/s should be carried and added with the digits of the next column.
Similarly, if one is following the double column method of addition then one would have to ‘write’ only two digits (which are at the extreme right position ) and the remaining digit/s should be carried and added with the digits of the next double column and so on .

A – 3 : The Double column method of addition becomes even more easy if the addition is done from the “tens”.

For example : 82 + 23 = ?

Solution : Say, 82 + 20 = 102
Then 102 + 3 = 105

This method may be used for the addition of any number of figures .

For e.g. 16 + 12 + 33 + 42 = ?

Solution : Say, starting from left side ; 16 + 10 ( of 12 ) = 26 and then 26 + 2 = 28 ; 28 + 30 ( of 33 )
= 58 and then 58 + 3 = 61 ; 61 + 40 = 101 .
Then 101 + 2 = 103 . Hence , the answer is 103 .

4)  For the addition of numbers containing decimals, the same procedure of 
 single (or double ) column method of addition should be used .

But some students may find it difficult to do so horizontally as the number of digits after the decimal point may not be same in different figures that are to be added .

This difficulty may be overcome by supplying Zeros at the end of every figure (excluding the figure having the largest number of digits after its decimal point ) so that every figure may have equal number of digits after its decimal point .

For e.g. : 836.32 +24.9751+1.2 = ?

Solution : In this question, the number of digits after the decimal point in first, second and third figures are two, four and one respectively.

Now, to balance the digits after decimal points, we supply two and three zeroes after the first and third figures respectively.
Now, the question looks like this :

836.3200 + 24.9751 + 1.2000 = ?

It can now be solved, without any confusion, with the help of the Double ( or Single ) column method of addition .

Procedure

(a) Underline the last two digits of every figure and add them i.e. 00 + 51 + 00 = 51. Write the last two digits of it ( here it is 51 ) and carry the remaining digits, if any .

(b) Underline the next two digits of every figure and add them i.e. 32 + 97 + 20 = 149 .
Write the last two digits of it ( here it is 49 ) on the left side of 51 and carry 1.

Now, the answer figure will become 4951.

(c) Underline the next two digits of every figure and add them i.e.1 ( carried from 149 ) + 36 + 24 + 1 = 62 .
Write the last two digits of the resultant on the left side of 4951 and carry the remaining digits, if any.

The answer figure becomes 624951 .

(d) Underline the next two digits of every figure and add them
i.e. 08 + 00 + 00 = 8
Now the answer figure becomes 8624951.

(e) Put the decimal point at the appropriate place. Here it is after four digits from the right side.
Hence, the answer is 862.4951.

Note : It is not necessary that one should always follow the double column method of addition . In fact, it depends on the student himself to decide which method (single column or double column ) he should apply so that the given problem may be solved quickly and easily. One can do it with a little of practice.

Some Examples

(1) 124 + 87 + 3794 = ?

Solution :

By Single Column Method

(a) Say, 4 + 7 + 4 = 15. Write 5 and carry 1.
(b) Say, 1 ( carried ) + 2 + 8 + 9 = 20. Write 0 on the left side of 5 and carry 2. Now the answer figure becomes 05.
(c) Again say, 2 (carried) +1+ 7 = 10 . write 0 on the left side of 05 and carry 1 . The answer figure becomes 005.
(d) Then say, 1 ( carried ) + 0 + 0 + 3 = 4. Write it on the left hand side of 005. Hence, the answer is 4005.

or By Double Column Method

Underline the first two digits of every figure and say 20 + 80 + 90 = 190 and 4 + 7 + 4 = 15

Now, 190 + 15 = 205 . Write 05 and carry 2.

Underline the next two digits of every figure, if any, and add 

them.

2 ( carried ) + 1 + 37 = 40. Write it on the left side of 05. So the answer figure becomes 4005. This is the answer.

(2) 72.3 + .901 + 873.2 = ?

Solution :

Put Zero at the end of every figure ( excluding the one having the largest number of digits after its decimal point ) 

       Now problem shall look like this : 72.300 + .901 + 873.200 

Underline the last two digits of every figure and add them .
+ 01 + 00 = 01. Write it ( i.e. 01 )

Again, Underline the next two digits of every figure and add 

them .
23 + 9 + 32 = 64 . Write it on the left side of 01.

       Now, the answer figure becomes 6401.

       (d)   Again underline the next two digits of every figure and add them . 

                          7 + 0 + 87 = 94.  Write this 94 on the left side of 6401.

                          The answer figure becomes 946401 .

(e) Now put the decimal point at the appropriate place .

The answer is 946.401.

SUBTRACTION

S – 1 : Like addition, subtraction should also be done horizontally and not longitudinally. Though some students may find if difficult, yet one can master the skill with a little practice and save a lot of one’s precious time while taking up the actual examination paper.

Example -1 : 378 – 199 = ?

Solution : By Single column method of subtraction :
(a) Say, 18 – 9 = 9. Write it .
(b) Again Say, 16 – 9 = 7. Write 7 on the left side of 9 .

Now the answer figure becomes 79.

(c) Now say, 2 – 1 = 1. Write it on the left side of 79 . Hence, the answer is 179 .

Note : Further explanation may be given for the above problem . See , in the first step we have to subtract 8 from 9 which is not possible as 8 is smaller than 9. So, take 1 from the next digit ( i.e. 7 ) to make it 10.

Now, 18 – 9 = 9 and 7 becomes 6 after giving 1 to 8 .

Similarly, in the second step we have to subtract 6 from 9 which again is not possible. So again take 1 from the next digit ( i.e. 3 ) to make it 16 .
Now, 16 – 9 = 7 and 3 becomes 2 after giving 1 to 7 .
So, in the third step we subtract 2 from 1 .

Example – 2 : 9202 – 3987 = ?

Solution : ( a ) Say, 12 – 7 = 5 Write it .
( b ) Again Say, 9 – 8 = 1 Write it on the left side of 5.
So the answer figure becomes 15.
( c ) Now say 11- 9 = 2. Write it on the left side of 15.
( d ) Lastly , 8 – 3 = 5. Write it on the left side of 215.
Hence, the Answer is 5215.

Note : In the first step, in the above question, we could not take 1 from Zero so we would have to take 1 from 20 and this 20 becomes 19 after giving 1 to 2.

Example – 3 : 7240 – 5970 = ?

Solution : By Double column method of subtraction :

         (a) Say, 140 - 70 = 70. Write it.

(b) Again Say, 11 – 9 = 2. Write it on the left side of 70.
(c) Lastly, 6 – 5 = 1, Write it on the left side of “ 270.
Hence, the answer is 1270.

Note : In the first step, in the above question, we could not
subtract 40 from 70, so we would have to take 1 from the
next digit ( i.e. 2) to make it 140 .

Example – 4 : 0.3568 – 0.3204 = ?

Solution : By Double Column method of subtraction first underline the last two digits of both the figures. Then,

(a) Say, 68 – 04 = 64. Write it.
(b) Again Say, 35 – 32 = 3. Write it on the left side of 64. So the Answer figure becomes 364.
(c) Now put decimal point at the appropriate position.

Here, it should be put after four digits from the Right side.
Hence, the Answer is .0364.

S – 2 : Like addition, subtraction also becomes even more easy if we do it from the “tens”.

For example, the subtraction of 47 from 88 can be done more quickly if we mentally increase the number to be subtracted to the nearest multiple of 10 ( i.e. increase 47 to 50 by adding 3 to it ) .

Similarly, mentally increase the other figure ( 88 ) also by the same amount ( i.e. 88 + 3) so that the value may remain unchanged .

Now, it is easy to subtraction 50 from 91 to get the answer i. e. 41. The whole process may be shown like this :

S – 3 : Sometimes, in subtraction, it is more suitable to decrease the number to be subtracted to the nearest multiple of 10 .

For example, the subtraction of 22 from 67 can be done more easily by decreasing 22 to 20 than by increasing it to 30.

Here, one should note that the other figure should also be decreased by the same amount ( here it is 2 ) so that the value may remain unchanged.

The whole process may be shown like this :

S – 4 : Use of “ Condition” for subtraction

Use this method when it is asked to find out what must be added to a number to make a second number .

Example -1 : 48 + 18 + 72 + ? = 150

Solution :

By the Single column method : 

(i) Say, 8 + 8 +2 = 18.
add 2 to make 20 ; carry 2.

(ii) Say, 2 (Carried) + 4 +1 + 7 = 14
add 1 to make 15 .
Hence, the answer is 12.

Example – 2 : 7519 + 401 + ? – 10 = 8226

Solution :

By Double column method:

Say, 19 +1 = 20 and 20 - 18 = 2 ;  add 24 to make 26 .

(ii) Again Say, 75 + 4 = 79 ; add 3 to make 82.

Hence, the answer is 324.

MULTIPLICATION

Multiplication of Certain kind of numbers can be done more quickly by the methods described below than by the conventional way of multiplication.

M – 1 : Multiplication by 5, 25, 125 and 625 can be done quickly by the following method :

To multiply by 5, use 10/2 ( i.e. place 1 Zero & divide by 2 ) .

To multiple by 25, use 100/4 ( i.e. place 2 Zeros & divide by 4 ) .

To multiple by 125, use 1000/8 ( i.e. place 3 Zeros & divide by 8 )

To multiple by 625, use 10000/16 ( i.e. place 4 Zeros & divide by 16 )

Example – 1 : 2124 x 25 = ?

Solution : 212400/4 =53100.

Example – 2 : 320 x 625 = ?

Solution : 320,0000 / 16 = 200000.

M – 2 a : Multiplication of ‘Cognate numbers’ .

Cognate numbers are those whose last digits together total 10 and
whose previous parts are exactly the same .

Example – 1 : 36 X 34 = ?

Solution : The above numbers are cognate as the unit figures together (6+4) total 10 and the
other digits are the same.
We can solve the above problem quickly by the following method :

Multiply the last digits of both the figures ( i.e. 6  x 4) and write their product (i.e. 24). This is the  

right part of the answer.
(b) Then multiply the remaining digit by one more than itself.
So,3 x (3+1) = 12. This is the left part of the answer. So write it on the left side of 24.

                                  The whole process can be shown like this : 

36 x 34 = 3 x ( 3 + 1) / 6 x 4 = 3 x 4 / 6 x 4 = 1224 . Hence, the answer is 1224.

Example – 2 : 994 x 996 = ?

Solution : 99 x ( 99 + 1 ) / 4 x 6 = 990024

Example – 3 : 104 x 106 = ?

Solution : 10 x ( 10 + 1 ) / 4 x 6 = 11024

Example – 4 : 898 x 892 = ?

Solution : 89 x ( 89 +1 ) / 8 x 2 = 801016

       Note :    In this method the right part of the answer should always  have two digits .

For Example, in the multiplication of 19 by 11, the left part of the answer is 1 x ( 1 + 1 ) = 2 and the right part of the answer is 9 x 1 = 9.

However, the right part of the answer should be written 09 and not 9.

So, 19 x 11 = 1 x 2 / 9 x 1 = 209 .

Example – 5 : 199 X 191 = ?

Solution : 19 x 20 / 9 x 1 = 38009 .

Example – 6: 999991 X 999999 = ?

Solution : 99999 x 10,0000 / 1 x 9 = 999990000009.

M – 2b : The method described in M – 2a can also be used for the multiplication of the numbers whose right two, three or four digits together total 100, 1000 or 10000 respectively.

In this method also, the only thing that we have to be careful is the number of digits in the right side of the answer figure.

When we take into consideration the right two digits of the multiplier and of the multiplicand, we are considering a total of four digits, so , the right part of the answer will have four digits.

Similarly, when we consider the last three digits of the multiplier and of the multiplicand, we are considering a total of six digits. Hence, the right part of the answer will have six digits.

Examples

(a) When the right two digits of the multiplier and of the multiplicand together total 100 and other digits are the same :

101 x 199 = 1 x ( 1+1) / 1 x 99 = 20099.
109 x 191 = 1 x (1 + 1 ) / 9 x 91 = 20819.
1081 x 1019 = 10 x (10 +1 ) / 19 x 81 = 1101539.

(b) When the right three digits of the multiplier and the multiplicand together total 1000 and other digits are the same :

1001 x 1999 = 1 x (1+1) / 999 x 1 = 2000999.

M – 2C : The method described in M-2a can also be used for the multiplication of fraction whose fractional parts together total 1 and the integral parts are the same.

Examples

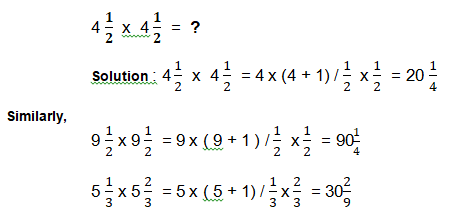
M – 3a : Multiplication of numbers whose last digits ( i.e. unit digits) together total 5 and other digits are the same .

Example – 1. 42 X 43 = ?

Solution :

Multiply the digits at the unit place (i.e. last digits ) of the multiplier and the multiplicand ( i.e. 2 x 3 ) and write it 

( 06 ) .
This is the right part of the answer.
(b) For obtaining the left part of the answer add the product of the multiplier and the multiplicand with one half of the multiplier.
The whole process can be shown like this :

42 x 43 = 4 x 4 +1/2 x 4 and 2 x 3 = 1806.

Example – 2 : 804 x 801 = 80 x 80 + 1/2 x 80 and 4 x 1 = 644004.

Example – 3 : 703 x 702 = ?

   703 x 702 = 70 x 70 + 1/2 x 70 and 3 x 2  =  493506.

Example – 4 : 1002 X 1003 = ?

        1002 X 1003 = 100 X100 + 1/2 x 100 and 2X3  = 1005006.

Example – 5 : 9001 x 9004 = ?

9001 x 9004 = 900 X 900 +1/2 x 900 and 1 x 4 = 81045004

M – 3b : In all the above examples of M-3a, we have considered only those numbers whose non – unit digits are even. But sometimes the non-unit digits of numbers may be uneven also . The procedure for solving such problems would be slightly different .

Example – 1 : 52 x 53 = ?

Procedure

(a) Multiply the digits at the units places (i.e.last digits) of the multiplier and the multiplicand ( i.e. 2 x 3 ) and write it ( 06 ) .

This is the right part of the answer.

(b) For obtaining the left part of the answer, first multiply the remaining digit/s of the multiplier and the multiplicand ( i.e. 5 x 5 = 25 ) and then divide the remaining digit/s of the multiplier by 2 ( i.e 1/2 x 5 = 2.5 ).

(c) Now, add 2 of 2.5 with 25.

(d) .5 of 2.5 should always be considered as 50 and added to the right part of the answer ( i.e. 06 ) .
The whole process can be shown like this :

 52 x 53 = 5 x 5 + ½ x 5 and 2 x 3 

= 25 + 2.5 and 06 = 25 + 2 and 50 (.5 taken as 50 )

06 = 27 and 56
Hence, the answer is 2756.

Example – 2 : 251 x 254 = ?

Solution : 251 x 254 = 25 x 25 +1/2 x 25 and 1 x 4
= 625 + 12.5 and 50 (.5 taken as 50 ) + 04
= 637 and 54
Hence the answer is 63754.

Example – 3 : 112 x 113 = ?

Solution : 112 x 113 = 11 x 11 + ½ x 11 and 2 x 3

= 121 + 5.5 and 06 = 126 and 50
( .5 taken as 50 ) + 06

 Hence, the answer is 12656.

Example – 4 : 972 X 973 = ?

Solution : 972 x 973 = 97 x 97 +1/2 x 97 and 2 x 3
= 945756

M – 3C : Multiplication of numbers whose last two digits together total 50 or 20 and the other digits are the same .

Example – 1 : 223 X 227 = ?

Solution : In the above question, the last two digits of multiplier and of multiplicand together total 50 ( i.e. 23 + 27 ) and the other digits are the same.

Procedure

(a) Multiply the last two digits of multiplier and
Multiplicand ( i.e. 23 x 27 = 621 ) and write the product.
This is the right part of the answer .

(b) For obtaining the left part of the answer, add the product of the remaining digit/s of the multiplier and of the multiplicand with one half of the remaining digits of multiplier.

The whole process can be shown like this :

 223 x 227 = 2 x 2 + ½ x 2 and 23 x 27 = 50621.

Example – 2 : 1421 x 1429 = ?

Solution : 1421 x 1429
= 14 x 14 + 1/2 x 14 and 21 x 29 = 2030609.

Example – 3 : 2311 X 2339 = ?

Solution : 2311 x 2339 = 23 x 23 +1/2 x 23 and 11 x 39

= 529 +11.5 and 429 = 5405429.

Similarly, when the last two digits of the multiplier and the multiplicand together total 20, the procedure is almost the same as described in Example -1 ( M – 3c ).

The only difference would be that in the step (b) of the procedure , the product of the remaining digit/s of the multiplier and the multiplicand would be added with the one fifth of the multiplier (and not one half of the multiplier) .

Example – 1 : 511 x 509 = ?

Solution : 511 x 509 = 5 x 5 + 1/5 x 5 and 11 x 9 = 26 and 0099 = 260099 .

Example – 2 : 412 X 408 = ?

Solution : 412 x 409 = 4 x 4 + 1/5 x 4 and 12 x 8 = 16 + 080 and 96 = 168096

Similar procedure can be applied when the last two digits of the multiplier and the multiplicand together total 40, 60 or 150.

When the total is 40

Example : 528 x 512 = ?

Solution : 528 x 512 = 5 x 5 + 2/5 x 5 and 28 x 12 = 270336.

When the total is 60

Example : 239 x 221 = ?

Solution : 239 x 221 = 2 x 2 + 3/5 x 2 and 39 x 21 = 52819

When the total is 150

Example : 475 x 475 = ?

Solution : 475 x 475 = 4 x 4 + 3/2 x 4 and 75 x 75 = 225625

M – 3d : The methods described in M – 3a can also be used in mixed fractions, when the fractional parts add up to 1/2 and the integral parts are the same .

Example –

M – 3e : The following quick method of multiplication should also be taken into general use. It helps in doing much of the multiplication mentally.

(1) 12 x 23 = ?

   Solution  :  23 x 10  = 230 and 23 x 2 = 46

   The answer is 230 + 46 = 276

(2) 14 x 12 = ?

Solution : 14 x 12 = 12 x 12 and 12 x 2 = 144 and 24 =144 + 24 = 168

(3) 16 x 15 = ?

Solution : 16 x 15 = 〖16〗^2 – 16 = 256 -16 = 240

(4) 21 x 34 = 20 x 34 + 34 = 680 + 34 = 714

(5) 23 x 45 = 20 x 45 + 45 x 3 = 900 + 135 = 1035

SQUARES

SQ – I : To find square of two digit numbers beginning with 5 (i.e. for numbers of 50 to 59)

Examples :

Q.1 52² = ?

Prucedure

Square the right part of the number ( i.e. 2 ) to get the right part of the answer. So, 2^2 = 4.

       Write 04 (The right part of the answer will always have two digit ).

To obtain the left part of the answer, square the left figure of the 

number ( i.e. 5 ) and add it with the right figure of the original number.

So, 5^2 + 2 = 27. Write 27 on the left of 04. Hence, the answer is
2704.

Similarly,

Q.2 〖54〗^2 = ?

Solution : 〖54〗^2 = 5^2 + 4 and 4^2 = 2916

Q.3 〖56〗^2 = 5^2 + 6 and 6^2 = 3136

Q.4 〖59〗^2 = 5^2 + 9 and 9^2 = 3481

SQ – 2: To find Square of numbers ending in 5.

Examples

Q.1 〖25〗^2 = ?

Procedure

Square the right part of the number ( i.e. 5 ) to get the right part of answers .

Multiply the left digit/s with one more than itself / themselves to obtain the left part of the answers .

So, 2 x ( 2 + 1) = 6
Write this 6 on the left of 25.

Hence, the answer is 625.

Similarly,

Q.2 〖45〗^2 = ?

Solution : 〖45〗^2 = 4 x 5 and 25 = 2025

Q.3 〖775〗^2 = ?

Solution : 〖775〗^2= 77 x 78 and 25 = 600625

Q.4 〖99995〗^2 = ?

Solution : 〖99995〗^2 = 9999 x ( 9999 + 1 ) and 25 = 9999000025

Q.5 〖95〗^2 = ?
Solution : 〖95〗^2 = 9 x 10 and 25 = 9025.

DIVISION

Division should be done either horizontally or longitudinally, whichever way the problem is written in the actual examination paper. For example, consider the division of 180 by 15.

In the actual examination paper, it will be written in either of the following ways :

180 ÷ 15     or      180/15 

For solving this problem most of the students shall first write it in the conventional way i.e. 15) 180 and then solve it.

This Practice is very time consuming as one wastes one’s time simply in writing the problem in a different way.

Also, While doing calculations, one should do as much work mentally as possible and in turn save the precious time during the actual examination.

For example, in the division of 180 by 15 :

Say, 18 ÷ 15 = 1. Write this 1 and carry the remaining 3 mentally.

Then, 30 ÷ 15 = 2 .

Write it on the Right side of 1. Hence, the answer is 12.

Division of Numbers Containing Decimal Point/s

D-1a : When the divider is greater than the dividend

In such Problems, first forget decimal point/s and do division. Then after completing the division we should put decimal point in the answer at the appropriate place.

The appropriate place of decimal point in the answer can be decided by subtracting the number of digits after the decimal point in the dividend from the number of digits after the decimal point in the divisor.

Examples

Q.1 0.0012 ÷ 0.6 = ?

Solution : First say, 12 ÷ 6 = 2 . Write it ( i.e. 2 only )

Here, we can see that the number of digits after the decimal point in the dividend (0.0012) is four and in the divisor (0.6 ) is one.
So, the answer is 0.002.
Q.2 0.018 ÷ 6 = ?

Solution : Say, 18 ÷ 6 = 3 Write it (i.e. 3 only)
Here, we can see that the decimal point is only in the dividend.

So count the number of digits after decimal point and accordingly put the decimal point in the answer figure.

The answer is 0.003.

Similarly :

• 0.046 ÷ .23 = 0.2
• 0.0126 ÷ .3 = 0.042
• 0.0364 ÷ 26 = 0.0014

D – 1b : When the divisor is lesser than the dividend.

Examples

Q.1 0.06 ÷ 0.002 = ?

Solution : First forget decimal point then Say, 6 ÷ 2 = 3 Write it .
Now, subtract the number of digits in the dividend (after decimal point ) from the number of digits in the divisor (after decimal point ) and then put as many zeros after 3 as much the difference of the digits comes.

Hence, the difference is 1 (i.e. 3 – 2 =1). So put one zero after 3 . Answer 30.

Q.2: 6 ÷ 0.002 = ? Answer 3000
Q.3 : 60 ÷ 0.002 = ? Answer 30,000.
Q.4 : 6.2 ÷ 0.002 = ? Answer 3100
Q.5 : 0.40 ÷ 0.2 = ? Answer :2
Note : In this problem, the last digit in the dividend is zero and it should not be considered while doing calculations for obtaining the appropriate place of the decimal point in the answer.
Q.6 : 6 .5 ÷ .0005 = 13000

Q.7 4.2 ÷ .2 = 21

Q.8 0.42 ÷ .2 = 2.1

Q.9 0.42 ÷ .002 = 210.

Q.10 42 ÷ .002 = 21000.

Q.11 4.2 ÷ .002 = 2100.

Q.12 2.50 ÷ .5 = 5 ( and not 50 )

FRACTIONS

F-1 : A fraction is a part of the whole and it must always be shown in its lowest terms i.e. the numerator and the denominator should not contain any common factor.

For example, the proper way of writing the fraction 14/21 would be 2/3 .

This is done by dividing both the numerator and the denominator by their common factor.

Here, the common factor of 14 and 21 is 7.

So, 14 ÷ 7 = 2

   21 ÷ 7 = 3

F – 2a :

ADDITION & SUBTRACTION OF FRACTIONS

Examples

Q.1 2/( 3 ) + 1/( 5) = ?

Solution : (a) For getting the numerator part of the answer, multiply transversely .

( i.e. 5 x 2 and 3 x 1 ) and then add them .

For getting the denominator part of the answer multiply 

the denominators of both the fraction ( i.e. 3 X 5 ) .
So the answer is 13/( 15)

The whole process can be shown like this :

(2 x 5 + 3 x 1)/(3 x 5) = 13/( 15)

Q.2 3/( 7 ) – 1/( 4) = ?

Solution : For subtraction of fractions the process is exactly the same as described in example (1) except that we do subtraction instead of addition for getting the numerator part of the answer.

The whole process can be shown like this :

3/( 7 ) – 1/( 4) = (4 x 3 – 7 x 1)/( 7 x 4 ) = (12 – 7)/( 28) = 5/( 28 )

F – 2b : When the denominators of the fractions, to be added / subtracted, are the same :

In such cases , for getting the numerator of the answer simply add / subtract the numerators of the fractions to be added / subtracted and either of the denominators of the fractions would be the denominator of the answer fraction.

Examples

Q.1 2/( 5 ) + 1/( 5) = ?

Solution : 2/( 5 ) + 1/( 5) = (2 + 1)/( 5 ) = 3/( 5)

So, the answer is 3/( 5) .

Q.2 2/( 5 ) – 1/( 5) = ?

Solution : 2/( 5 ) – 1/( 5) = (2 – 1)/( 5 ) = ( 1)/( 5)

Q.3 1/( 2 ) + 1/( 2) = ?

Solution : 1/( 2 ) + 1/( 2) = (1+1)/( 2) = 1

Q.4 1/( 3 ) + 1/( 3) + 1/( 3) = ?

Solution : 1/( 3 ) + 1/( 3) + 1/( 3) = (1+1+1)/( 3) = 1

Q.5 1/( 7 ) + 3/( 7) = ?

Solution : 1/( 7 ) + 3/( 7) = (1+3)/( 7) = 4/( 7)

Q.6 9/( 16 ) + 6/( 16) = ?

Solution : 9/( 16 ) + 6/( 16) = (9+6)/( 16) = 15/( 16)

Q.7 1/( 6 ) + 1/( 6) + 1/( 6) = ?

Solution : 1/( 6 ) + 1/( 6) + 1/( 6) = (1+1+1)/( 6) = 1/( 2)

Q.8 3/( 8 ) + 1/( 8) + 1/( 8) = ?

Solution : 3/( 8 ) + 1/( 8) + 1/( 8) = (3+1+1)/( 8) = 5/( 8)

Q.9 2/( 19 ) + 8/( 19) + 6/( 19) = ?

Solution : 2/( 19 ) + 8/( 19) + 6/( 19) = (2+8+6)/( 19) = 16/( 19)

Q.10 4/( 9) – 1/( 9) = ?

Solution : 4/( 9) – 1/( 9) = (4-1)/( 9) = 3/( 9)

Q.11 5/( 12) – 3/( 12) = ?

Solution : 5/( 12) – 3/( 12) = (5 – 3)/( 12) = 1/( 6)

( F – 2C )

Examples

Q.1. ( 3)/( 8) + ( 5)/( 64) = ?

Solution : ( 3)/( 8) + ( 5)/( 64) = ( 3 x 8)/( 8 x 8) + ( 5)/( 64) = ( 24)/( 64) + ( 5)/( 64)

= ( 24 + 5)/( 64) = ( 29)/( 64)

  Q.2    ( 2)/( 3)   -    ( 5)/( 12)   =  ?

Solution : ( 2)/( 3) – ( 5)/( 12) = ( 2 x 4)/( 3 x 4) – ( 5)/( 12) = ( 8)/( 12) – ( 5)/( 12) = ( 8 – 5)/12

= ( 3)/( 12) = ( 1)/( 4)

( F – 3 )

ADDITION OF A FRACTION WITH A NUMBER

Examples

Q.1 6 + ( 3)/( 5) = ?

Solution : In such cases, first multiply the denominator of the fraction with the number to be added and then add their product with the numerator.

Denominator of the answer would be the same as the denominator of the fraction.

In the above example :

Say, 5 x 6 = 30 . Then, 30 + 3 = 33 .

The answer is ( 33)/( 5) or 6( 3)/( 5) .

SHORT – CUT

As the answer of the above problem shows, we could get the answer directly simply by putting the number on the right side of the fraction which is to be added .

So, 6 + ( 3)/( 5) = 6 ( 3)/( 5)

Q.2 9 + ( 1)/( 5) = 9 ( 1)/( 5)

Q.3 16 + ( 9)/( 17) = 16( 9)/( 17)

Q.4 3 + 2( 1)/( 5) = 5( 1)/( 5)

Q.5 8 + 12( 3)/( 4) = 20( 3)/( 4)

Q.6 ( 1)/( 5) + 3 = 3( 1)/( 5)

Q.7 9( 2)/( 5) + 5 = 14( 2)/( 5)

Q.8 11( 1)/( 2) + 11 = 22( 1)/( 2)

( F – 4 )

Subtraction Of A Number From A Fraction ( & Vice Versa )

(a) When a number is to be subtracted from a fraction :

METHOD – 1

Examples

Q.1 2 – ( 3)/( 4) = ?

Solution : For obtaining the numerator of the answer, in such cases, first multiply the denominator of the fraction with the number and then subtract their product from the numerator of the fraction.

The denominator of the answer would be the same as that of the denominator of the problem fraction.

In the above example :

       Say, 4 X 2 = 8     &     8 - 3 = 5  .    

Hence, the answer is ( 5)/( 4) or 1( 1)/( 4)

Similarly,

Q.2 6 – ( 5)/( 8) = ?

Solution : 6 – ( 5)/( 8) = ( (8 x 6) – 5)/( 8) = ( 43)/( 8) = 5( 3)/( 8)

Q.3 15 – 2/( 3) = ?

Solution : 15 – 2/( 3) = ( (3 x 15) – 2)/( 3) = ( 43)/( 3) = 14( 1)/( 3)

Q.4 7 – 3/( 5) = ?

Solution : 7 – 3/( 5) = ( ( 5 x 7 ) – 3)/( 5) = ( 32)/( 5) = 6( 2)/( 5)

METHOD – 2 :

Examples

Q.1 12 – 2/( 5) = ?

The subtraction of the above type can be done even more quickly by the following method :

(i) Subtract the number by 1. Write that i.e. 12 – 1 = 11
(ii) For obtaining the numerator part of the answer, subtract the numerator of the problem fraction from its denominator. i.e. 5 – 2 = 3. This is the numerator of the answer fraction .

The denominator of the answer fraction would be the same as that of the problem fraction ( in the above problem it is 5 ) .
Hence, the answer is 113/( 5)

( In this way, you can solve the above problem or for that matter any of this kind of problems, without even using your pen. No ? )

Q.2 21 – 8/( 13) = ?

Solution : Say, 21 – 1 = 20. Again say, 13 – 8 = 5.

Hence, the answer is 205/( 13) .

(3) When a fraction is to be subtracted from a number :

Examples

Q.1 1/( 4) – 3 = ?

Solution : In such cases, for obtaining the numerator part of the answer, first multiply the denominator of the problem fraction with the number and then add their product with the numerator.

Denominator of the answer would be the same as that of the problem fraction .

The whole process, for the above problem, can be shown like this :

1/( 4) – 3 = (4 x ( -3 ) + 1)/( 4) = (-12 + 1 )/( 4) = (-11)/( 4) = -23/( 4)

Similarly,

Q.2 2/5 – 6 = ?

Solution : 2/5 – 6 = (5 x ( -6 ) + 2)/( 5) = (-30 + 2 )/( 5)
= (-28)/5 = – 53/( 5)

Q.3 12/15 – 2 = ?

Solution : 12/15 – 2 = (15 x ( -2 ) + 12)/( 15) = (-30+12 )/15

= (-18)/15 = – 11/( 5)

Q.4 7/11 – 2 = ?

Solution : 7/11 – 2 = (11 x ( – 2 ) + 7)/( 11) = (-15)/( 11)
= – 14/( 11)

Note : This kind of subtraction can also be solved even more quickly and easily than the method described above .

Examples

Q.1 2/( 3) – 129 = ?

Solution :

(i) Subtract the number by 1 . Write that i.e. 129 – 1 = 128 .

(ii) For obtaining the numerator part of the answer, subtract the numerator of the problem fraction from its denominator .

i.e. 3 – 2 = 1 . This is the numerator of the answer fraction .

The denominator of the answer fraction would be the same as that the problem fraction ( in the above problem it is 3 ) .

Hence, the answer is -1281/( 3) .

Note : In such cases, the answer would always be in negative .

Q.2 13/19 – 1265 = ?

Solution : Say, 1265 – 1 = 1264 . Again say, 19 -13 = 6

Hence, the answer is : -12646/( 19)

Q.3 21/23 – 6918 = ?

Solution : Say, 6918 – 1 = 6917 Again say, 23 – 21 = 2
Hence, the answer is : – 6917 2/23

In dealing with the mixed fractions, one should tackle the integral and the fractional parts separately.

M – F 1 :

Examples :

Q.1 5 1/( 3) + 2 1/( 6) = ?

Solution :

Add the integral parts i.e. 5 + 2  =  7 .  Write it .

Add the fractional parts and write the resultant on the Right side of 7.

i.e. 1/( 3) + 1/( 6) = 2/( 6) + 1/( 6) = 3/( 6) = 1/( 2)

Hence, the answer is 71/( 2) .

Q.2 63/( 5) – 4 1/( 3) = ?

Solution : (i) Subtract the integral parts. i.e. 6 – 4 = 2 . Write it.
(ii) Subtract the fractional parts and write the resultant on the Right side of 2.

i.e. 3/( 5) – 1/( 3) = (3 x 3 – 5 x 1)/( 5 x 3) = 4/( 15)

Hence, the answer is 24/( 15) .

Similarly ,

Q.3 121/( 4) + 103/( 8) = ?

= 12 + 10 and  (1 x 2)/█(4 x 2@) + 3/( 8)  = 225/( 2) = 241/( 2)

Q.4 21/( 3) + 41/( 3) + 31/( 3) = ?

= 2 + 4 + 3  and  1/( 3)+  1/( 3)+  1/( 3)=9+1=10

Q.5 185/( 12) + 3/6 + 51/( 2) = ?

= 18 + 5 and ( 5)/( 12)+ (3 x 2)/█(6 x 2@) + (1 x 6)/█(2 x 6@) = 2317/( 12) = 245/( 12)
Q.6 51/( 3) – 31/( 3) = ?

= 5 – 3 and 1/( 3) – 1/( 3) = 2 + 0 = 2

Q.7 112/( 3) – 51/( 3) = ?

= 11 – 5 and 2/( 3) – 1/( 3) = 61/( 3)

Q.8 54/( 6) – 31/( 2) = ?

= 5 – 3 and ( 4)/( 6) – (1 x 3)/( 2 x 3) = 21/( 6)

Q.9 83/( 14) – 51/( 7) = ?

= 8 – 5 and 3/( 14) – 1/( 7) = 31/( 14)

Q.10 – 43/( 7) – 71/( 8) = ?

= – ( 4 3/( 7) + 71/( 8) ) = – ( 1131/( 56) ) = – 1131/( 56)

Q.11 160/( 16) + 160/( 8) = ?

Solution : 160/( 16) + 160/( 8)= 160 ( 1/( 16) + 1/( 8) ) = 160 x 3/( 16) = 30

( M – F 2 )

Examples

Q.1 823/( 13) – 404/( 7) = ?

Solution : In the above problem, by the subtraction of the fractional parts , we get a negative sign as 3/13 is less than 4/( 7) .

So, the procedure for this kind of problems would obviously be different .

The procedure is as follows :

(i) Subtract the integral parts and reduce the resultant by 1 . i.e. 82 – 40 = 42 and then 42 – 1 = 41 .

This is the integral part of the answer.

(ii) Subtract fractional parts : 3/13 – 4/( 7) = – 31/( 91)

Now, subtract 91 from 31 to obtain the numerator of the answer fraction i.e. 91 – 31 = 60

The denominator of the answer fraction would be the same as that of the denominator of the fraction obtained in step (ii).

Hence, the answer is 4160/( 91) .

MULTIPLICATION OF FRACTIONS

Examples

Q.1 1/( 2) x 3/( 5) = ?

Solution : 1/( 2) x 3/( 5) = (1 x 3)/( 2 x 5) = 3/( 10)

Q.2 5/( 12) x 6/( 8) = ?

Solution : 5/( 12) x 6/( 8) = 5/( 2) x 1/( 8) = (5 x 1)/( 2 x 8) = 5/( 16)

Q.3 9/( 16) x 1/( 3) = ?

Solution : 9/( 16) x 1/( 3) = 3/( 16) x 1/( 1) = 3/( 16)

Q.4 33/( 4) x 12/( 11) = ?

Solution :      33/( 4)  x 12/( 11)  =  3/( 1)  x  3/( 1)  = 9

Q.5 5 1/( 2) x 2 1/( 2) = ?

Solution : 51/( 2)  x 2 1/( 2)  =  11/2  x 5/( 2)  = 55/4 = 133/4

Q.6 1 2/( 3) x 2 1/( 3) = ?

Solution :  1 2/( 3)  x 2 1/( 3)  =  5/3  x 7/( 3)  = 35/9 = 3 8/9

DIVISION OF FRACTIONS

Examples

Q.1 1/( 3) ÷ 2/( 5) = ?
Solution : 1/( 3) ÷ 2/( 5) = 1/( 3) x 5/( 2) = 5/( 6)

Q.2 61/( 4) ÷ 2 2/( 3) = ?

Solution : 61/( 4) ÷ 2 2/( 3) = 25/( 4) x 3/( 8) = 75/( 32) = 2 11/( 32)

Q.3 92/( 3) ÷ 1/( 12) = ?

Solution : 92/( 3) ÷ 1/( 12) = 29/( 3) x 12/( 1) = 116

Q.4 1/( 2) ÷ 3/( 5) ÷ 1/( 7) = ?

Solution : 1/( 2) ÷ 3/( 5) ÷ 1/( 7 ) = 1/( 2) x 5/( 3) x 7/( 1) = 35/( 6) = 55/( 6)

Q.5 2/( 5) ÷ 1/( 3) ÷ 6/( 5) ÷ 2/( 3) = ?

Solution : 2/( 5) ÷ 1/( 3) ÷ 6/( 5) ÷ 2/( 3) = 2/( 5) x 3/( 1) x 5/( 6) x 3/( 2) = 11/( 2)

Q.6 5 1/( 2) ÷ 2 3/( 5) ÷ 1/( 2) = ?

Solution : 5 1/( 2) ÷ 2 3/( 5) ÷ 1/( 2) = 11/( 2) x 5/( 13) x 2/( 1) = 55/( 13) = 43/( 13)

Quantitative Aptitude Part – 1

Quantitative Aptitude Part – 2