This study material is developed with a view to the latest examination pattern of various banking services and government  jobs . Every care is taken to solve questions through Shot – Cut  Methods  instead of traditional methods.

Quantitative Aptitude Study Material for Your Success

Course Content Quantitative Attitude Part – 1

Course Content Quantitative Attitude Part – 2

• SIMPLE INTEREST & COMPOUND INTEREST         

• AVERAGE           

• Time , Work & Wages , Pipe & Cistern    

• TIME & DISTANCE           

• STREAMS 

Course Content Quantitative Attitude Part – 3

Time-Saving Methods

• ADDITION          

• SUBTRACTION                  

• MULTIPLICATION            

• SQUARES            

• DIVISION                     

• FRACTIONS        

• ADDITION & SUBTRACTION        

• ADDITION  OF A FRACTION WITH A NUMBER     

• MIXED FRACTIONS         

• MULTIPLICATION OF FRACTIONS             

• DIVISION OF FRACTIONS

The job seekers should seriously follow the Time – Saving  Methods to quickly solve the questions in the actual examination and get success in getting their dream job ” – Director

BODMAS

[ , ( ) , of , ÷ , x , + , – , ]

For the simplification of the expressions which involves signs brackets, of, ÷, x, +, -, the rule of ‘BODMAS’ should be strictly followed.

In the word ‘BODMSA’ each letter is the initial letter of a word :

B Stands for Bracket

O Stands for off (i.e. ‘multiplication’)

D Stands for Division  

S Stands for Subtraction

M Stands for Multiplication

The order from the Left hand side should be strictly maintained.

Tips for Quickly solving simplification questions

•           Look for common factors that can be canceled out.

•           Use the distributive property to simplify expressions.

•           Remember that negative signs apply to the numbers immediately following them.

•           Be careful with the order of operations.

With practice, you will be able to solve simplification questions quickly and accurately.

Example :

Q.1   2 + 5 ÷ 5 =  ?

Solution :  2 + 5 ÷ 5 = 2 + 1 = 3  ( correct answer ) and Not  2 + 5 ÷ 5 = 7 ÷ 5  = 7 / 5 ( wrong answer ).

we need to perform the division first before we add the two numbers.

5 ÷ 5 = 1

So, 2 + 5 ÷ 5 = 2 + 1 = 3

Q.2   9 + 8 of 2 – 4 + 23 = ?

Solution :  9 + 16 – 4 + 23   = 48 – 4 = 44  ( ‘of’ = ‘multiplication’ ) .

Explanation:

According to the order of operations (BODMAS), 8 of 2 is done first since it is within a parenthesis. So, 8 of 2 is equal to 8 * 2 = 16.

Now we have 9 + 16 – 4 + 23.

Next, we simplify the expression from left to right. So, 9 + 16 = 25, and 25 – 4 = 21.

Finally, 21 + 23 = 44.

Therefore, 9 + 8 of 2 – 4 + 23 = 44.

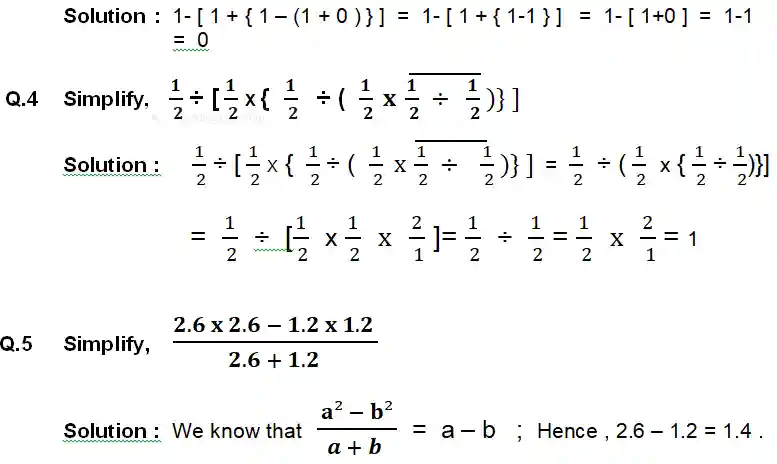
 Here,  a = 16.2 , b = 13.3 .       

Hence , the Answer is  2 .

SQUARE ROOT & CUBE ROOT

• SQUARE : If a number is multiplied by itself , the product is called the Square of  the number.

• SQUARE ROOT ( Vargmool ) of a number is that number which when multiplied by itself is equal the given number. Thus , 3 is the square root of 9 and 4 is the square root of 16 .

The Square root of a number is indicated by the symbol   √    or    √¯   .

Thus, √9 = 3 , √16 = 4 ,  √25 = 5 .

 ( √9  = √3×3 = 3 ; √16 = √4×4 = 4 ; √25 = √5×5 = 5 etc.)

 Note  :  The square root of 1 is 1.

Memorize the following Tables 

 It will help you in solving various types of problems quickly .

Table – 1

Number	Square	Number	Square	Number	Square
1	1	11	121	21	441
2	4	12	144	22	484
3	9	13	169	23	529
4	16	14	196	24	576
5	25	15	225	25	625
6	36	16	256	26	676
7	49	17	289	27	729
8	64	18	324	28	784
9	81	19	361	29	841
10	100	20	400	30	900

Table – 2

Number	Cube	Number	Cube	Number	Cube
1	1  (  ie.1 x 1 x 1 )	11	1331	21	9261
2	8	12	1728	22	10648
3	27	13	2197	23	12167
4	64	14	2744	24	13824
5	125	15	3375	25	15625
6	216	16	4096	26	17576
7	343	17	4913	27	19683
8	512	18	5032	28	21952
9	729	19	6859	29	24389
10	1000	20	8000	30	27000

Table – 3

√2  = 1.41421	√5  = 2.23607	√10  = 3.16
√3  = 1.73205	√7  = 2.65	√15  = 3.873

Table – 4

Since,   (0. 1)2   =  0.01	Hence   √0.01 = 0.1
Since,    (0. 8)2   =  0.64	Hence   √0.64 = 0.8
Since,    (0. 05)2 =  0.0025	Hence   √0.0025 = 0.05
Since,      (2. 5)2  =  6.25	Hence   √6.25 = 2.5
Since,    (0. 001)2 =  0.000001	Hence   √0.000001 = 0.001

Q.1      A General can draw up his regiment of 6889 men in the form of a solid square. Hence the number in the last row will be ?

Solution :  The number of men in the last row = √ 6889 = 83.

Since he can draw 6889 men in the form of a solid square, the number of soldiers in each row and column of the square will be equal to the square root of 6889 = 83.

Therefore, the number of soldiers in the last row will also be equal to 83.

So the answer is 83.

Q. 2     A General wishing to draw up his 16160 men in the form of a solid square, found that he had 31 men over. Find the number of  men in the front row.

Solution :      Since the general wants to put 16160 men in the form of a square and he could arrange only 16160 – 31 men in that form i.e. 16129 men could be arranged.

So, the number of men in front = √16129 =127.

Explanation:

To form a solid square, we need to arrange the men in a square array, with the same number of men in each row and column. The number of men in the front row is equal to the number of rows in the square.

We can use the following equation to find the number of rows in the square, s, given the total number of men, n, and the number of men left over, r:

_S2=n−r

Substituting the given values, we get:

_S2=16160−31=16129

Taking the square root of both sides, we get:

s=127

RATIO & PROPORTION

The number of times one quantity contains another quantity of the same kind is called the ratio of the two quantities.

Clearly, a ratio may be expressed in the form of a fraction. A ratio, for example, of Rs.5/- and Rs. 7/- may be expressed either in the form  5 : 7 or in the form 5 / 7.

Proportion is an Equality of Ratios.

Explanation:

A proportion is an equality of two ratios. In other words, two ratios are said to be in proportion if the two ratios are equal.

For example, the ratio of 2 to 4 is equal to the ratio of 6 to 12. This can be written as 2:4 = 6:12.

The equality of two ratios can be denoted by the symbol “:=”. For example, the two ratios 2:4 and 6:12 can be written as 2:4 : = 6:12.

Proportions are used in many different areas of mathematics, including geometry, algebra, and trigonometry. They can also be used in everyday life, such as when comparing prices or calculating discounts.

For example, 15 : 45 = 1 : 3 or 15/45 = 1/3 .

Each of these expressions indicates a proportional.

The terms 15 , 45, 1, 3 are distinguished as the 1st , 2nd , 3rd and 4th proportional respectively.

Another example is the ratio of 1 hour to 60 minutes. This is equal to the ratio of 2 hours to 120 minutes. This can be written as 1:60 = 2:120.

The Ist and 4th proportional are called ‘Extremes’ .

The 2nd and 3rd proportional are called the ‘Means’ .

In the above proportional, it is clear that  15 x 3 = 45 x 1 .

So,       

Product of the Extremes  =  Product of the Means   

In a proportion, the product of the extremes is always equal to the product of the means. This is a property of proportions that is known as the product of means and extremes theorem.

The extremes are the first and last terms of the proportion, while the means are the middle terms. For example, in the proportion 2:3::4:6, the extremes are 2 and 6, while the means are 3 and 4.

The product of the extremes is 26 = 12. The product of the means is 34 = 12. Therefore, the product of the extremes is equal to the product of the means.

This property can be used to solve problems involving proportions. For example, if we are given that 2:3::x:y, we can solve for x and y by setting up the equation 2x = 3y.

The product of means and extremes theorem is a useful tool in mathematics. It can be used to solve problems involving proportions, as well as to understand the properties of proportions.

Solution :       If X be the required mean proportional , then 8 : X : : X : 2 

( Multiply Means & Extremes )

or   X² = 8 x 2

Hence , X =  4  

Q.5   If 12 : X = X : 3, then X = ?

Solution :  X² =  12 X 3   =  36      ,     

Hence,  X   =  6  

Explanation :

using the product of means and extremes theorem.

The product of the means = The product of the extremes

(12)(3) = (X)(X)

36 = X^2

X = 6 or -6

Since X is positive, X = 6.

Therefore, the value of X is 6.

Here is the detailed solution:

• We are given that 12 : X = X : 3.
• Writing this as a proportion, we get 12/X = X/3.
• Multiplying both sides of the equation by X, we get 12X = X^2.
• Subtracting X^2 from both sides of the equation, we get 12X – X^2 = 0.
• Factoring the left-hand side of the equation, we get X(12 – X) = 0.
• This means that either X = 0 or 12 – X = 0.
• Since X cannot be 0, X = 12 – X.
• Solving for X, we get X = 6.

Q.6    If 15 boys can do a piece of work in 120 days, in how many days will 18 boys  do it ?

Solution ( SHORT CUT )         

Since the number of “boys days” required to complete any piece of work is always the same, so :

The number of boys x The number of days in Ist case  = The number of boys x The number of days in 2nd case

Hence, 15  x 120  =  18 x X          

or          X   =  144 days

Explanation:

The number of boys and the number of days required to complete a work are inversely proportional. This means that if the number of boys increases, the number of days required decreases.

Let x be the number of days required for 18 boys to complete the work.

We have the following proportion:

15 : 18 : : 120 : X

Simplifying the proportion, we get:

18 x 120 = 15 x X

2160 = 18X

X = 2160/18

X = 144

Therefore, it takes 144 days for 18 boys to do the work.

 Q.7     If 12 men working 4 hours a day for 120 days can complete a piece of work, how many men working 6 hours a day for 12 days will be needed ?

Solution ( SHORT – CUT )

Since the number of “ man day hours” need to complete the work in both the cases is the same so,

12 x 4 x 120  = X x 6 x 12  

X = (12 x 4 x 120) / (6 x 12)

X = 40

    So, 40 men are required.

Q.10    A garrison of 1200 men has provision for 15 weeks. If at the end of 5 weeks they are reinforced by 300 men, how long will the provision last ?

 Solution ( SHORT – CUT )

At the end of 5 weeks, the food for 1200 men is left for (15 – 5) i.e. 10 weeks.

At this stage, the number of men are 1200 + 300 = 1500.

So, we have to find out if 1200 men can have the food in 10 weeks, then how long 1500 men will take to consume the same food .

 If X is the required number , then :

1500 : 1200  = 10 : X       

or         X =  1200 x 10 / 1500 = 8 Weeks or 56 days 

So, the provision will last for 8 + 5 = 13 weeks.

The garrison has provision for 1200 men for 15 weeks. So, the total number of men that the provision can support is 18000 (1200 x 15).

After 5 weeks, the number of men in the garrison is 1200. The provision that was supposed to last for 15 weeks will now last for 12000/1200 = 10 weeks.

300 more men are added to the garrison. So, the total number of men in the garrison is 1500.

Let x be the number of weeks that the remaining provision will last.

1500X = 12000/10

X = 8

Therefore, the remaining provision will last for 8 weeks.

However, there is a catch here. The question says that the reinforcement of 300 men happened after 5 weeks. So, the 5 weeks of provision that the initial 1200 men had is not included in the 8 weeks that the remaining provision will last.

So, the remaining provision will last for 8 + 5 = 13 weeks.

Q.11   If 20 men can build a wall 40 meters long, 4 meters high and 0.4 meter thick in 15 days, in how many days will 25 men build a wall 30 meters long, 4 meters high and 0.4 meters thick .

Q.13    If 1/18 : X = 9 : 4 , find the value of X .

To find the value of X in the proportion 1/18 : X = 9 : 4, we can set up a cross-multiplication equation and solve for X.

The given proportion can be written as:

(1/18) / X = 9 / 4

Now, cross-multiply:

1/18 x 4 = 9 x X

Simplify the left side:

4/18 = 9 x X

Now, solve for X:

X = (4/18) / 9 X = 4/162 X = 2/81

So, the value of X is 2/81.

Q.14    If 2/5 : 3 = 14 : X , find the value of X .

Solution : 2 : 5 x 3 = 14 : X               

or           X  = 5 x 3 x 14 / 2   = 105

Q.17   What is the ratio whose terms differ by 70 and the measure of which is 7/42.

Solution :    X / X + 70   =  7 / 42      or        42X  =  7 ( X+70 ) = 7 X + 490       

or       X  = 490 / 35 = 14

Hence , Ratio is X  :  X  +  70  =  14 : 84

Alternative  Method  ( SHORT – CUT  )  

When the difference between the two terms of the given Fraction 7/42  is  35 , the first term is 7. So, when the difference between the two terms of the ratio is 70 the first term would be   x 70 = 14  and the second term of the ratio  would be 14 + 70 = 84.

.           The Answer is 14 : 84

COMPOUND RATIO

Ex.1.   Find the ratio compounded of the four ratios :

2 : 6,   8 : 18,   12 : 16,   5: 9

Solution :

To find the compounded ratio, we multiply the ratios together.

2/6 x 8/18 x 12/16 x 5/9 = 64/39

Therefore, the compounded ratio is 64 : 39.

Ex.2.   Compound ratio of 16 : 4, 4 : 2, 18: 6 is = ?

Solution :

o find the compounded ratio, we multiply the ratios together.

16/4 x 4/2 x 18/6 = 180/1

Therefore, the compounded ratio is 180 : 1.

Q.18    In a town there are 94,500 people. 2/9 of them are Muslims, 6400 are Christians and the rest are Hindus.  How many are Hindus ?

Solution (SHORT – CUT )

Out of the total 94,500 people 2/9 of them are Muslims. So, the total number of Christians and Hindus would be 94,500 x  = 73,500 and the number of Hindus in the town would be 73,500 – 6,400 = 67,100.

Explanation:

The number of Muslims in the town is 2/9 x 94500 = 22000.

The total number of Christians and Hindus is 94500 – 22000 = 72500.

Since the rest of the population are Hindus, then the number of Hindus is 72500 – 6400 = 66100.

So the answer is 66100.

Q.19    The product of two numbers is 1452. The first number is 1/3rd of the second number. Find the first number.

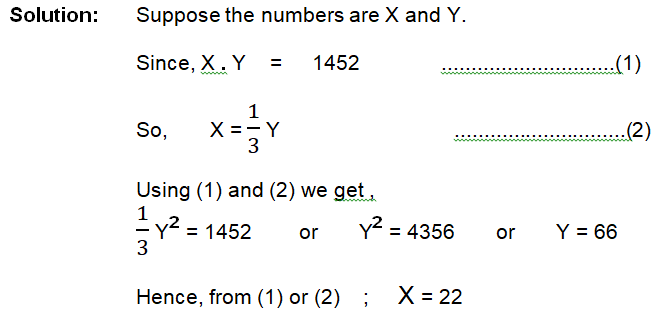
Q.20    If A : B = 5 : 9 and B : C = 3 : 2, What is :

• A : C and
• A : B : C

The combined proportion can be obtained by 5 x 3, 9 x 3 and 9 x 2 . i.e. 15 : 27 : 18  or  5 : 9 : 6

Q.21    The marks obtained by Praveen and Vijay are in the ratio of 4 : 5 and the marks obtained by Vijay and Suresh are in the ratio 3 : 2 . Therefore, What is the ratio of the marks obtained by Praveen and Suresh ?

Q.22    A third of Kamala’s marks in Mathematics equals a half of her marks in Science. If she obtained 60 marks in the two subjects together, how many marks did she get in science ?

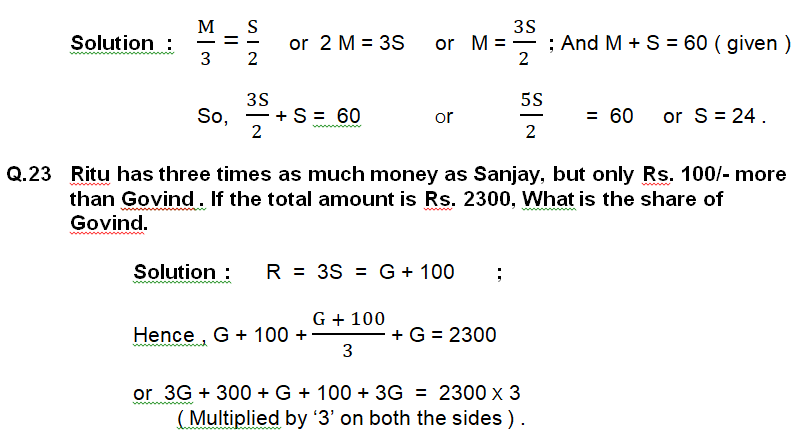
or      7G + 400 = 2300 X 3       

or       G  = 6900 – 400 / 7 =  928.57

Q.24   Rs. 48 is divided into two parts such that 7 times the first part added to 5 times the second part make 246. What is the first part ?

Solution :   Let the first part be X and the second part be 48 – x.

We are given that 7x + 5(48 – X) = 246.

Simplifying the equation, we get 12X = 156.

X = 13.

Q.25   Anupam has Rs. 12 more than Ranjan and Rs. 9 more than Pankaj . All the three have Rs. 33 in all . What is the share of Anupam .

Solution :     

Let Pankaj’s share be X.

Then, Ranjan’s share = X + 9.

And, Anupam’s share = X + 9 + 12 = X + 21.

We know that the total amount is Rs. 33.

So, X + X + 9 + X + 21 = 33

3X + 30 = 33

3X = 3

X = 1.

Therefore, Pankaj’s share = Rs. 1.

Ranjan’s share = Rs. 1 + 9 = Rs. 10.

And, Anupam’s share = Rs. 1 + 9 + 12 = Rs. 22.

So the answer is 22.

Q.26   Rs. 4800 are distributed among A, B and C in ratio of 6 : 5 : 4. What is the difference in the shares of A and C .

Solution :     

A’ s share =  x 4800 = Rs. 1920     

C’ s share =   x 4800 = Rs. 1280

The difference between A’ s and C’ s shares is Rs. ( 1920 – 1280 )  =  Rs. 640 .

SHORT – CUT : ( Using Unitary Method )

When the total is 15 ( ie. 6+5+4 = 15 ) , the difference between the share’s of A and C =  2  ( ie. 6 – 4 = 2 )

When the total is 1 the difference between the share’s of A and C  =  2/15

When the total is 4800 the difference between the share’s of A and C   =   2/15 x 4800  =  640 .

Q.27    On Monday, Rahul read twice the number of pages he read on Tuesday. On Wednesday, he read half of the total number of pages of what he read on Monday and Tuesday. If he read 60 pages in all, how many pages did he read on Monday ?

Let the number of pages read by Rahul on Tuesday be X.

Number of pages read on Monday = 2X

Number of pages read on Wednesday = (1/2) * (2X + X) = X

Total number of pages read = 60

2X + X + X = 60

4X = 60

X = 15

Therefore, Rahul read 2X = 2 x 15 = 30 pages on Monday.

So the answer is 30.

Q.28    Two numbers are in the ratio of 4 : 7 . If 8 be subtracted from each , then they are in the ratio of 2/5. Find the second number .

Solution :      Let the numbers be 4X and 7X       

Hence ,   4X – 8 / 7 X – 8 =  2 / 5   

or   5 ( 4X – 8 ) = 2 ( 7X – 8 )

or   20X – 40 = 14 X – 16     

or      X = 4

Hence, the Second number ( 7 X ) = 7 x 4 = 28 .

Q.29   The ratio of Murali’s age to Raju’s age is 4 : 7 and the sum of their ages is 55 years. What will be the ratio after 10 years .

Solution :      Let their ages be 4X and 7X .

So, 4X + 7X = 55   Or   X = 5   ;   Murali’s age = 4 x 5 = 20   &   Raju’s age   = 7 x 5 = 35

Now, after 10 years their ages would be 20  + 10  =  30 and 35 + 10 = 45.

Hence, the answer is 2 : 3 .

Q.32  2/3 of a number is 20 less than the original number. What is the number ?

Solution    :   Let the number be X .

Now ,  X – 2X / 3   =   20    

or         X / 3 = 20    

or   X   =  60

Q.33   The sum of three numbers is 132 . If the first number be twice the second and the third number be half the first, what is the second number ?

Solution ( SHORT – CUT )

Let the second number be X.

Then, the first number is 2X and the third number is X/2.

We know that the sum of the three numbers is 132.

So, X + 2X + X/2 = 132

11x/2 = 132

X = 24

Therefore, the second number is 24.

So the answer is 24.

Q.34    Divide a certain sum of money between A and B so that B gets 3/5 of what A gets . If B gets Rs. 1050, then what is the share of A .

Solution :  Suppose A gets X then B gets 3X/5  which equal to Rs. 1050 .    

Hence, X = 1750/-

Q.35    What C will get out of Rs. 660 if A gets twice as much as B and B gets thrice as much as C ?

Solution ( SHORT – CUT ):  Suppose C gets Rs. 1.

Then, naturally, the share of B would be Thrice of 1 ( i.e. 3 ) and that of A would be 3 x 2 = 6

Therefore, the share of C, out of 660, would  be  =   1 x 660 / 6 + 3 + 1  =  66

PERCENTAGE

(Percentage -1) : A fraction, whose denominator is 100, is called the rate percentage ( or percentage ) and the numerator of the fraction is denoted by % .

A percentage is a fraction whose denominator is 100. It is denoted by the symbol “%”.

For example, 25% is equivalent to the fraction 25/100, which is equal to 0.25.

The word “percentage” comes from the Latin phrase “per centum”, which means “out of one hundred”.

• Percentages are used to express parts of a whole. For example, if a test has 100 questions and you answer 80 correctly, you have scored 80%.

• Percentages can also be used to compare two different quantities. For example, if the price of a product increases by 10%, it means that the new price is 110% of the old price.

For example, 25% means 25 out of 100

This can be expressed as   25 / 100   = 1 / 4     

Similarly, 100% means      100 / 100    = 1

 Percentage – 2 :

(A)       Multiply by 100 if you want to show a certain number in  % .

Examples :

Q.1       2 / 10   as a rate per cent is ?

Solution :      2 / 10  x 100 = 20%

Explanation:

To express a fraction as a percentage, you should multiply the numerator by 100 and place a percent sign (%) after it.

2/10 x 100 = 20.

Hence, 2/10 as a rate per cent is 20%.

Q.2    3.793 as a rate per cent is ?

Solution : 3.793 x 100 = 379.3 %

Explanation:

To express a decimal as a percentage, you should multiply it by 100 and place a percent sign (%) after it.

In this case, 3.793 x 100 = 379.3.

Therefore, 3.793 as a rate per cent is 379.3%.

More Details:

A percentage is a number or ratio expressed as a fraction of 100. It is denoted by the symbol “%”.

To express a decimal as a percentage, we multiply it by 100 and place a percent sign (%) after it.

In the case of 3.793, multiplying it by 100 gives us 379.3. So, 3.793 as a rate per cent is 379.3%.

Here is another way to look at it. 379.3% is equivalent to 379.3 per hundred. This means that 379.3 is 379.3 out of every 100.

(B)    Divide by 100 if you want to remove % sign from a certain number .

Examples :

Q.1     20% = ?

Solution :   20 / 100  = 1 / 5    

Q.2    3.768 % = ?

Solution :   3.768 / 100     =  0.03768 

 Percentage Rule – 3        

100%  =  1 ( i.e. Whole of anything )

200%  =  two times of anything

400%  =  four times of anything.

Similarly,

50% =   1 / 2  of anything

25% =  1 / 4  of anything

20%  =   1 / 5 of anything

10%  = 1 / 10  of anything

Examples :

100% of 10 will be 10  x  1  =  10	200% of 10 will be 10  x  2  =  20	400% of 10 will be 10  x  4  =  40
50% of 10 will be   10  x  1 / 2  =  5	25% of 10 will be  10  x  1 / 4 =  2.5	10% of 10 will be  10  x  1 / 10  =  1

  Percentage – 4 : In examinations, the questions based on the following relationship of A, B  and C, are often asked :

     A  %  of  B  = C  

In such problems, one is required to find out the value of any of the three ( i.e. A, B or C ) on the basis of the given values of any two .

These problem can be easily solved in the following way :

A = C x 100 / B

B = C x 100 / A

C = A x B / 100

Examples :

Q.1   Find out the value of X if X % of 200 is equal to 50 .

Solution :      X  =  50 x 100 / 200  =  25

Explanation:

X% of 200 = 50

To solve for X, we can first rewrite the percentage as a fraction:

X/100 of 200 = 50

Then, we can multiply both sides of the equation by 100:

X of 200 = 5000

This gives us:

200X = 5000

Dividing both sides of the equation by 200, we get:

X = 25

Therefore, the value of X is 25.

In other words, 25% of 200 is equal to 50.

Q.2   20 is what % of 80 or X % of 80 is 20 ?

Solution  :     X = 20 x 100 / 80 =  25%

Explanation:

The statement “20 is what % of 80” can be written as an equation as follows:

X% of 80 = 20

To solve for X, we can first rewrite the percentage as a fraction:

X/100 of 80 = 20

Then, we can multiply both sides of the equation by 100:

X of 80 = 2000

This gives us:

80X = 2000

Dividing both sides of the equation by 80, we get:

X = 25

Therefore, 20 is 25% of 80.

Q.3      40% of 600 is equal to what ?

Solution :        Suppose, 40% of 600 = X .

  Hence,    X =  40 x 600 / 100 =  240

Explanation:

To calculate 40% of 600, we can first rewrite the percentage as a fraction:

40 / 100 of 600

Then, we can simplify the fraction:

2 / 5 of 600

Now, we can multiply 600 by 2/5:

600 x 2/5 = 240

Therefore, 40% of 600 is equal to 240.

Memories the following relationships given in the Chart below. It will help you in solving the percentage questions quickly :

CHART-1 :

5% = 1/20	15% = 3/20	12   % = 1/8	25 % = 1/4
10 % = 1/10	35 % = 7/20	% = 3/8	50 % = 1/2
20 % = 1/5	45 % = 9/20	62   % = 5/8	75 % = 3/4
40 % = 2/5	55 % = 11/20	% = 7/8	100 % = 1
60 % = 3/5	65 % = 13/20
80 % = 4/5	85 % = 17/20

From the above chart we can see that for obtaining 5% of a certain number, we have to divide the number by 20 and so on .

Examples :

 Q.1     5% of 80 = ?

Solution  : 80 X 1/20 = 4

Explanation:

To calculate 5% of 80, you can first rewrite the percentage as a fraction:

5/100 of 80

Then, you can simplify the fraction:

1/20 of 80

Now, you can multiply 80 by 1/20:

80 * 1/20 = 4 X

Therefore, 5% of 80 is equal to 4.

 Q.2     20% of 400 = ?

Solution  : 400 X 1/5 = 80

Q.3   35% of 900 = ?

Solution  :  900 X 7/20 = 315

Q.4   12.5% of 200 = ?

Solution  :  200 X 1/8  = 25

Similarly,

 (1)      If  5%  of   X   = 10  then ,     100 % of   X  = 10 x 20 = 200

 (2)      If 10 % of X   = 30 then ,      100% of X     = 30 X 10 = 300

 (3)      If 20% of  X = 25 then ,        100%  of  X = 25 x 5  =  125

(4)      If 35% of X      = 70 then ,      100% of X = 70 X 20/7 = 200

(5)     If 12.5% of X = 50 then ,     100% of X =    50 x 8 = 400

 (6)      If 25% of  X        = 50 then ,  100% of X = 50 X 4 = 200

Some Examples

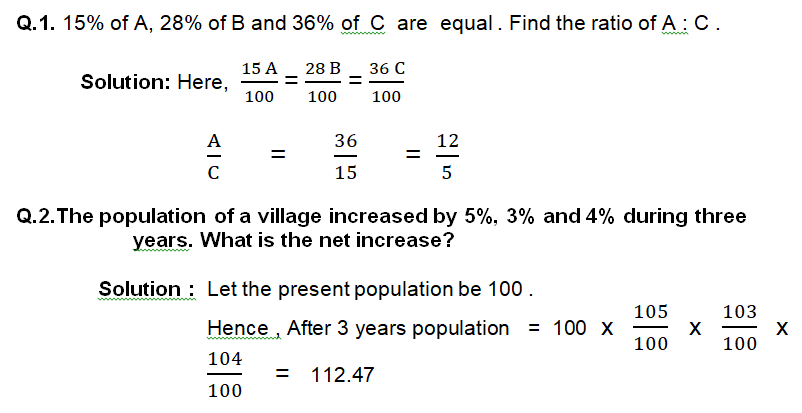
Q.3. If A gets 130% of B & B gets 95% of C then A gets what % of C ?

Solution  :    

Given that A gets 130% of B and B gets 95% of C.

130% of B = 130/100 * B = 13B/10 95% of C = 95/100 * C = 19C/20

Therefore, A = 13B/10 = (13B/10) / (19C/20) x 100% of C = 91.11% of C

So, A gets 91.11% of C.

Q. 4. A man saves 20% of his income of Rs. 20,000 per month . How much does he spends ?

Solution :      He spends 100% – 20%  =  80% .    

Hence, Rs. 20,000 x 4/5 =  Rs. 16,000/-

Explanation:

The man’s monthly income is Rs. 20,000 and he saves 20% of it, so his savings is 20/100 * 20000 = Rs. 4000.

Therefore, the amount he spends is 20000 – 4000 = Rs. 16000 per month.

Q. 5. The population of a town has increased from 50,000 to 70,000. Find the increase per cent .

Solution ( RULE ) : Increase % = Total Increase / Original  X  100

Hence , Increase % = 20,000 / 50,000  x 100 = 40 %

Explanation:

The population of the town has increased by 20,000 (70000 – 50000).

The percentage increase is calculated by dividing the increase in population by the original population and multiplying by 100%.

Percentage increase = (20000/50000) x 100% = 40%

Q. 6.    A man loses 10% of his money and after spending 60% of the remainder, has Rs. 3600 left. How much had he at first ?

Solution :      Suppose he had Rs. X at first .

Then,  X x 90 / 100 x 40 / 100 = Rs. 3600    

or    X = Rs. 10,000 .

Q. 7.  A woman has a certain number of mangoes, of which 10% are bad . She gives 60% of the remainder in charity and then has 36 left . How many she had at first ?

Solution  :

Suppose she had X mangoes at first .

10% of X are bad, hence she gives 60%  of 90 X / 100 in charity and 40% of it is left .

So, the whole process can be shown like this :

 X  x   90 / 100 x 40 / 100  =  36            

or           X   =  100 mangoes

Q. 8.  Two numbers are respectively 20% and 40% more than a  third number. What is the ratio of the two numbers ?

Solution :      Suppose the third number is 100.

Hence, the Ist and IInd numbers would naturally be 120 and 140 respectively.

Ratio = 120 : 140 = 6 : 7.

Explanation:

Let the third number be x.

The first number is 20% more than x, so it is equal to 1.2x.

The second number is 40% more than x, so it is equal to 1.4x.

The ratio of the first number to the second number is:

1.2x / 1.4x = 6/7

Therefore, the ratio of the two numbers is 6:7.

Q. 9. A Regiment lost in an engagement 25% of its men and still had 300 men left . What was the original number of men in the regiment ?

Let the original number of men in the regiment be X.

25% of X is equal to the number of men lost, so 0.25X = 300.

X = 300 / 0.25

X = 1200

Therefore, the original number of men in the regiment is 1200.

Q. 10. The number of seats for admission for a vocational course is   increased by 15% every year. If the number of students in 2017 is 800, what is the expected number of students in 2019 ?

Solution :  

The number of seats for admission for the vocational course is increased by 15% every year.

In 2018, the number of seats will be 800 x 115/100 = 920

In 2019, the number of seats will be 920 x 115/100 = 1048

Therefore, the expected number of students in 2019 is 1048.

Q. 11.  30% of A’ s salary is equal to the 20% of 3/5th of B’ s salary. If B’s salary is Rs. 24,000/- , what is  A’s salary ?

Solution :   Suppose A’s salary is Rs. X.

Then,  3X / 10  =  1 / 5   x   3 / 5    x  24000/-       

( 30% = 3/10,  20% = 1/5 )

or      X = Rs. 9600/-

Q. 12.  In a library, 40% of the total number of books are in English, 80% of the rest in Hindi and the balance 300 books are in other languages. What is the total number of books in the library ?

Q. 13. After deducting 20% from a certain sum and then  25% from the remainder, there are Rs. 1200/-  left .  Find the original sum .

Solution :      Suppose the original sum was Rs. X.   After deducting 20%, 80% of X is left .

Then after deducting 25% of the remainder 75% of it would be left which is equal to Rs. 1200/-

The whole process can be shown like this :  4X / 5 x 3 / 4 = 1200    ( 80% = 4 / 5  , 75% = 3 / 4

or    X  =  Rs. 2000

Q. 14. In an examination on English and Hindi there are 130 candidates. If 70% passed in both the subjects, how many failed in at least one subject ?

Solution  : 30% of 130 should have failed in at least one  subject  i.e. 39  candidates .

Q. 15. In an examination 7500 students appeared. Each offered either Physics or Chemistry or both. If 75% offered Physics and 45% Chemistry, how many offered both ?

Solution :     

75% of the 7500 students offered Physics and 45% offered Chemistry.

The number of students who offered Physics is:

7500 x 75/100 = 5625

The number of students who offered Chemistry is:

7500 x 45/100 = 3375

Let the number of students who offered both Physics and Chemistry be x.

Then, 5625 + X + 3375 – X = 7500

X = 375

Therefore, 375 students offered both Physics and Chemistry.

Q. 16.   In an examination A scored 115 marks which were 5 marks less 40%. How many marks did B secure if B  scored 65% ?

Solution :  40% of X (marks)  = 115 + 5 = 120

X  =  120 x 5/2 = 300  ( Since, 40% of X  =  2/5 of X 

Hence , 100% of X = 5/2 of X )

Now, B secures  = 300 X 65/100  = 195 marks

Q. 17.  In an examination, 34% of the total number of candidates failed and the number of those who passed exceeded the number of those who failed by 64. Find out the total number of candidates.

Solution  :    Suppose, the total no. of candidates = 100 .  

Then, 66% – 34% = 32%     

Since, 32% = 64   ( By Unitary Method )

1% = 64/32% .  

Hence, 100% = 64/32 X 100 = 200

Q. 18.  In an examination 38% marks are required to pass. A candidate secured 38 marks and failed by 38 marks. Find out the maximum marks .

Solution :      38% = 38 + 38 = 76   ;   100% =  x 100  = 200

Short Cut :    In this type of questions, if all the three figures i.e. per cent required to pass, marks obtained by the candidate and marks required to pass are same (as in this question), the answer would always be 200.

Q. 19.  The population of a town was 7000. During the year men increased by 10% while women by 5%. The population at the end of the year increased to 7850. Find original number of men and women.

Solution : ( SHORT – CUT )

Suppose all were men .

Since, 10% of 7000 = 700  .   But the actual increase is 850 . 

So, 850 – 700 = 150 is 5% of women. 

Hence, 100% of women = 150 x 20 = 3000 . 

And Men = 7000 – 3000 = 4000 .

Q. 20.  At an election , 20% voters did not cast their votes, one of the two candidates secured 40% of the polled Votes and lost by a margin of 960. Find  (i) Total votes and  (ii) polled votes.

Given that 20% of the voters did not cast their votes, so 80% of the voters cast their votes.

Let the total number of votes be X.

Number of votes polled = 80% of X = 80X / 100 Given that one of the two candidates secured 40% of the polled votes and lost by a margin of 960 votes.

So, the other candidate secured 60% of the polled votes and won the election by a margin of 960 votes.

Hence, 60% of 80X/100 = 960 => 96X/100 = 960 => X = 10000

(i) Total votes = 10000

(ii) Polled votes = 80% of 10000 = 8000 votes.

So the answer is 10000, 8000

Q.21.  If 500 ml. of water is added to 1 liter of a solution of 15% alcohol in water, what is the % strength of alcohol in the final solution ?

Solution  :     In 1000 ml. solution alcohol is 15%.  

In 1500 ml. solution alcohol  = 15 x 1000 / 1500 = 10%.

Explanation:

In the initial solution, there is 15% alcohol by volume, which means that there are 0.15 * 1000 = 150 ml of alcohol in 1 liter of solution.

When 500 ml of water is added, the total volume of the solution becomes 1000 + 500 = 1500 ml.

The amount of alcohol remains the same, so there are still 150 ml of alcohol in the 1500 ml solution.

The % strength of alcohol in the final solution is:

(150 ml / 1500 ml) x 100% = 10%

So the answer is 10%.

Q. 22.  A reduction in the prices of oranges enables a person to purchase 3 oranges for Rs. 100 instead of Rs. 125. What is the percentage reduction in price ?

Solution :      Reduction on Rs.125    =   Rs. 25 .  

 So,  % reduction = 25 x 100 / 125 =  20 %.

Explanation:

The original price of 3 oranges is Rs. 125. So, the original price of 1 orange is Rs. 125/3 = Rs. 41.67.

The new price of 3 oranges is Rs. 100. So, the new price of 1 orange is Rs. 100/3 = Rs. 33.33.

The percentage reduction in price is:

(41.67 – 33.33) / 41.67 x 100% = 20%

Therefore, the percentage reduction in price is 20%.

Q. 23.  The daily wages of a worker increased by 20% but the number of hours worked by him per week dropped by 20%. If he was originally getting Rs. 1000 per week, what would he get per week now ?

Solution :      Suppose, X and Y are original wages and number of hours  respectively.

So,       X x Y = 100

120 X / 100 x 80 Y / 100 = 96 XY / 100

i.e. He will get 96% of Rs. 1000 which is equal to Rs. 960.

SHORT – CUT

In this type of questions there will always be a loss as the increase in wages and decrease in number of hours is the same .

RULE :

Q. 24.   The price of sugar increases by 20% . By what % must a housewife reduce the consumption of sugar, so that the expenditure on sugar is the same as before ?

Solution :      Suppose, previously the price of sugar was Rs. 100 per Kg. and the consumption 100 Kg.

Now, if X Kg be the reduced consumption,  100 X 100 = 120 x X      

or          X = 83.33

Hence, the housewife must reduce consumption by 100 – 83.33 = 16.6 %

Q. 25.  The price of an article is increased by 40%. In order to restore the original price, the new price must be reduced by how much % ?

Solution :      If original price is Rs. 100 , new price is Rs. 140.

Hence, the new price must be reduces by 140 – 100 / 140  x 100  =  28 and 4 / 7

Explanation:

Let the original price of the article be $100. The new price after a 40% increase = 100 + 40% of 100 = $140 To restore the original price, the new price must be reduced by $140 – $100 = $40. The percentage by which the new price must be reduced = (40 / 140) * 100% = 28.57%

Therefore, the new price must be reduced by 28.57% in order to restore the original price.

Q. 26.  When duty on a commodity is reduced by 20% the consumption increase by 15%. By how much % is the revenue from the commodity increased or decreased ?

Solution ( RULE )

Revenue  =  Tax x Consumption

Here, Revenue = 80%  x 115 %   =   92.00% .  

Hence , the Decrease % =  8% .

PARTNERSHIP

An association in which two or more than two persons associate to invest money and carry on a certain business is called a Partnership .

A partner who manages the business is called a ‘ Working Partner ’ while the one who provides capital but does not attend to the business is called a ‘Sleeping Partner’.

Profit (or loss) in a business is shared in proportion to the capitals contributed by each taking into consideration the time for which the capital of each remained in the business.

When the time for which the various investments are in the business is different, we find out the “monthly equivalents” of the investments, by multiplying the investments with the number of months for which they are in the business.

Example 1. A and B are partners in a business and they together invested Rs.20,000,00/-. At the end of the year, of a  total profit of Rs. 2,00,000, A’ s share was Rs. 80,000. What was A’ s investment  ?

Solution : Since, profits are divided in the ratio of the investments of the partners.

When , the total investment is 2 + 3 = 5 , A’s investment is 2 

When the total investment is 1 , A’s investment will be 2/5

Hence, when the total investment is 20,00,000/- ,

A’s investment will be =     2/5  x Rs.20,00,000 = 8,00,000/-                                

Example  2.  Ranjan started a shop by investing Rs. 12,000, Sudhir joined him 4 month’s later , investing Rs. 7000. At the end of one year they earned a profit of Rs. 13,300. What will be Dinesh’s share of profit ?

Ranjan invested Rs. 12000 for 12 months, while Sudhir invested Rs. 7000 for 12 – 4 = 8 months. So, the ratio of their investments = (12000 * 12) : (7000 * 8) = 144 : 56 = 9 : 4 Ranjan’s share of the profit = 13300 * (9/13) = Rs. 9900

So the answer is 9900.

Example 3.   A and B enter into partnership with capital in the ratio of 5 : 6 . At the end of 10 months A withdraws. If they receive profits in the ratio of 5 : 8 ,  find how long B’s capital was used ?

Solution :      The capital ratio of A to B is 5 : 6.

The profit ratio of A to B is 5 : 8.

Let the duration for which B’s capital was used be b months.

Then, (5 x 10) / 6 x b = 5 / 8 => b = (5 x 10 x 8) / (6 x 5) = 6.25.

So, B’s capital was used for 6.25 months.

Example 4.   A’s share in a business is 3/4th of B’s share . B got a profit of Rs. 1200 by investing Rs. 40,000 in the business. What will be the ratio of A’s profit to his investment in the business ?

Solution: Let the total profit be X. Since B’s share is 1200,

A’s share = X – 1200 A’s share is 3/4th of B’s share => (3/4) X 1200 = X – 1200 => X = 1800

A’s profit = 1800 – 1200 = 600

The ratio of A’s profit to his investment = 600 / 10000 = 3/5

Therefore, the ratio of A’s profit to his investment in the business is 3 : 5.

Example 5. Three partners A, B and C invest Rs. 14,000, Rs. 16,000 and Rs. 20,000 respectively in a business. How should they divide a profit of Rs. 4000 ?

Solution :      The profit should be divided in the ratios of the Capitals, that is,  in the ratio of 7 : 8 : 10

Now, 7 + 8 + 10  =  25

Hence,  A’s share  7/25  x  4000   =  Rs.1120   

B’s share  8/25  x  4000   =  Rs.1280

C’s share 10/25 x  4000   =  Rs.1600

Example 6.   A is a working and B is a sleeping partner in a business. A puts in Rs.80,000/- and B puts in Rs. 1,20,000/-.  A receives 10 % of the profit for managing the business and the rest is divided in proportion to their capitals . What does each get out of a profit of Rs.10,000 /-.

Solution :

• A’s share for managing the business = 10% of Rs. 10000 = Rs. 1000
• Remaining profit = Rs. 10000 – Rs. 1000 = Rs. 9000
• Ratio of A’s capital to B’s capital = 80000 : 120000 = 2 : 3
• A’s share of the remaining profit = 2/5 * 9000 = Rs. 3600
• B’s share of the remaining profit = 3/5 * 9000 = Rs. 5400
• Therefore, A gets a total of Rs. 1000 + Rs. 3600 = Rs. 4600
• And B gets a total of Rs. 5400

So, A gets 4600 rupees and B gets 5400 rupees.

PROFIT AND LOSS

( PL – 1)        If the selling price ( S.P. ) of an article is more than the cost price ( C.P. )  of  the  article, then there is a gain .

  Gain  =  S.P. – C.P.  

( PL- 2 )          If S.P. is less than the C.P. , then there is a loss.

Loss =  C.P. – S.P.

Similarly,

   In a business, if there is a loss, then :  

S.P. = CP. ( 100 – Loss % ) / 100

C.P. = SP x 100 / 100 – Loss %

                           In short ,  the above relation can be written like this :

  S.P. x 100 = C.P. [ 100 + Gain ( or Loss ) ]  

Example 1.   A man buys 10 apples for Rs. 300 and sold each for Rs. 40/- . What is his  gain or loss  percentage .

Solution :      C.P. of 10 apples = Rs. 300

S.P. of 10 apples = Rs. 400  .    

Hence, Gain %    = x 100  =  33.33

Explanation:

The man bought 10 apples for Rs. 300, so the cost price of each apple is 300/10 = Rs. 30/- He sold each apple for Rs. 40/-, so he made a profit of 40 – 30 = Rs. 10/- on each apple. The profit percentage is 10/30 * 100% = 33.33%

Therefore, the man made a profit of 33.33%.

Example 2. A car is sold for Rs. 5,00,000 at a gain of 25% . What was the cost price of  the car ?

Solution :      S.P.  =   125 %  of  C.P. =  Rs. 5,00,000 /-

 C.P.   =   5,00,000 / 125  x 100   =    Rs. 4,00,000 /-

Explanation:

The car was sold at a gain of 25%, so the cost price was 500000 / 1.25 = Rs. 400000.

In other words, the cost price was 100% and the selling price was 125%.

Example 3.  A merchant purchased 5 quintals of sugar for Rs. 2900/- and spend Rs.45 ontransport, 5 paisa per Kg. as Octroi duty and Rs. 30 as Coolie charges. He sold the sugar at Rs. 6.30 per kg. What was his gain % ?

Solution  :     C.P. of 5 quintals of Sugar = Rs. 2900/- .     

Transport paid   = Rs. 45

Octroi duty paid at 5 paise per Kg for 5 quintals ( or  500 kg ) = Rs. 25

Coolie charges paid     =    Rs.30

Net Cost price for 500 kg.    =    Rs. 3000/- .

i.e.    C.P. for 1 kg of Sugar  = Rs. 6

S.P. for 1 kg of Sugar  =   Rs. 6.30

Hence, Gain %   =   0.30 x 100 / 6  = 5 

                           

Example 4.  By selling an article sheetal earned a profit equal to the 1/4^th  of the price he bought it. If he sold it at Rs.375, what was the cost price ?

Solution: Let the cost price of the article be Rs. X.

The profit earned is 1/4 x X.

The selling price is Rs. 375.

Therefore, we have the equation:

X + (1/4) x X = 375

5/4 x X= 375

X = 281.25

Therefore, the cost price of the article is Rs. 281.25.

Example 5. There would be 15% loss if an article is sold at Rs.340/- . At what price it must be sold to gain 10% profit ?

Let the cost price of the article be Rs. x.

Selling at Rs. 340/- results in a loss of 15%.

Therefore, the cost price is 115% of Rs. 340/-.

X = (115/100) x 340

X = 391

To gain 10% profit, the selling price should be 110% of Rs. 391/-.

Selling price = (110/100) x 391

Selling price = 429.1

Therefore, the article must be sold at Rs. 429.1/- to gain 10% profit.

Example 6. Rakesh marks his goods 20% above cost price but allows 5% discount for cash . What per cent profit does he really make ?

Solution  :     If the cost price is Rs.100 the marked price  =  100 + 20   =   Rs.120

Discount    =    5%  of  Rs.120   = Rs. 6

Net S.P.    =    Rs. 120 –  Rs. 6  =  Rs. 114 .  

So, gain    =    14%

Example 7. 6% more is gained by selling an article for Rs. 300 than by selling for Rs. 288. What is the cost price of the article .

Solution: Let the cost price of the article be Rs. X.

Selling the article for Rs. 300 gives a profit of 6% more than selling it for Rs. 288.

Therefore, the profit obtained by selling the article for Rs. 300 is Rs. 6/100 x 288 = Rs. 17.28.

The total profit obtained by selling the article for Rs. 300 is Rs. 300 – X.

Therefore, we have the equation:

300 – X = 17.28

X = 282.72

Therefore, the cost price of the article is Rs. 282.72.

Example 8.  Pankaj buys two books at Rs. 40 each. He sells one at a gain  of 10% and  the other at a loss of 10 % . What is his gain or loss % .

Solution  :    

Let’s say the cost price of each book is Rs. 100.

When he sells one book at a gain of 10%, he gets a profit of Rs. 10.

When he sells the other book at a loss of 10%, he incurs a loss of Rs. 10.

The total profit on one book and the total loss on the other book cancel each other out. However, there is a loss due to undercasting, which is calculated as follows:

Loss due to under casting = Common loss or gain percentage x Common loss or gain percentage / 100

In this case, the common loss or gain percentage is 10%.

Therefore, the loss due to under casting is: 10 x 10 / 100 = 1%

Example 9. A book seller sold two books at Rs. 40 each. He sold one book at a loss of 10% and the other at a gain of 10%.What is his gain or loss % ?

Let the cost price of the first book be CP1 and the cost price of the second book be CP2.

The selling price of the first book is 40 rupees and the loss incurred is 10%, so the cost price is:

CP1 = (100/90)*40 = 44.44 rupees

The selling price of the second book is also 40 rupees and the profit made is 10%, so the cost price is:

CP2 = (100/110)*40 = 36.36 rupees

The total cost price of the two books is CP1 + CP2 = 44.44 + 36.36 = 80.8 rupees.

The total selling price of the two books is also 40 + 40 = 80 rupees.

Since the total selling price is equal to the total cost price, the book seller made no profit or loss.

Hence, the gain or loss percentage is 0%.

Example 10. The selling price of 50 articles is equal to the cost price of the same 60 articles. What is the per cent gain of loss ?

Solution :      C.P. of  60 = S.P. of 50 = Rs. 60 ( say ) .

C.P. of  50 =  Rs. 50 .      Gain  =    Rs. 10

Gain%   =   10/50 x 100  =   20%

Note: If the selling price of 50 articles is equal to the cost price of the same 40 articles, then the trader made a loss of 20%.

Example 11. A man sold a Calculator for Rs. 300 and lost something. Had he sold it for Rs. 345 his gain would have been double the former loss. What is the cost price ?

Solution  :      If X be the loss, then :

  300 = C.P. – X                     ……….(1)

  345 = C.P. + 2 X                 ……….(2)

45     =  3 X              ( on subtraction of 1 & 2 )

or  X =  15 .                Hence, C.P.= Rs.315

Example 12. What price should a tradesman mark on an article which costs Rs.153 to gain 20% after allowing a discount of 15% ?

Solution :      Suppose marked price is X .

So, 85%  of  X = 120% of 153      

 or      85 / 100 . X    =  120 / 100 x 153  =  Rs. 216

Example 13. If the selling price of 4/5 of a number of articles be equal to the cost price of the whole, what is the profit percentage ?

Solution  :     Suppose, the cost price is Rs. 100

4/5 x S.P. = 100       or        S.P.  =   100 x 5/4   = Rs. 125   

Hence , Gain %  = 125 – 100 = 25.

Therefore, the profit percentage is 25%.

Example 14. A horse was sold at a loss of 10%. If it was sold for Rs. 70/-  more, there would have been a gain of 4%. Find C.P. ?

Let the cost price of the horse be Rs. x.

• When the horse is sold at a loss of 10%, the selling price is 90% of x.
• When the horse is sold at a gain of 4%, the selling price is 104% of x.

The problem states that the selling price of the horse is Rs. 70/- more when it is sold at a gain of 4% than when it is sold at a loss of 10%.

=> 104% of X – 90% of X = 70

=> 4% of X = 70

=> x = 70 x 100 / 4 = Rs. 1750/-

Therefore, the cost price of the horse is Rs. 1750/-.

Example 15. A shopkeeper buys 12 pencils for Rs. 10 and sells 10 pencils for Rs. 12. How much profit he earns ?

The cost price of 1 pencil = 10/12 = Rs. 5/6 The selling price of 1 pencil = 12/10 = Rs. 6/5 The profit per pencil = 6/5 – 5/6 = 1/30 The profit percentage = (Profit per pencil / Cost per pencil) * 100 = (1/30) / (5/6) * 100 = 6.66%

Therefore, the shopkeeper earns a profit of 6.66%.

Example 16.  If the cost price of 18 pens is equal to the selling price of 15 pens, find out the  profit .

There is no profit in this case, but a loss of 3 pens.

Let the cost price of one pen be x.

The cost price of 18 pens is 18x.

The selling price of 15 pens is also 18x.

So, the loss is 18x – (15x) = 3x.

In percentage terms, the loss is:

Loss% = ( Loss / Cost price) x 100%

= (3x / 18x) x 100% = 16.67%

Therefore, there is a loss of 3 pens with a loss percentage of 16.67%.

Example 18. A dishonest dealer professes to sale his goods at 1000 gms. cost price, but uses a weight of 900 gms. for a Kilogram  weight . What is his real gain per cent ?

Solution :

Example 20. A sells an article to B for Rs. 11,000 at a gain of 10% and B sells it back to  A loss of 10%. So What is the gain per cent of A ?

Let the cost price of the article for A be Rs. X.

So, A sold the article to B at a gain of 10% = 110% of X = Rs. 11,000

=> 110/100 x X= 11000

=> x = 10000 When B sells the article back to A at a loss of 10%,

Selling price = 90% of Rs. 11000 = Rs. 9900

So, the overall gain of A = 9900 – 10000 = Rs. 900

Gain percentage = (Gain / Cost price) x 100%

= (900 / 10000) x 100% = 9%

Therefore, the overall gain percentage of A is 9%.

Quantitative Aptitude Part – 2

Quantitative Aptitude Part – 3